dB
· A decibel (dB) is a unit of measurement used to express the ratio of powers, sound pressures or other things on a logarithmic scale.
· The decibel was invented by Bell Labs and named after Alexander Graham Bell.
· In this tutorial the decibel is used to express the ratio of electrical powers (meaning Watts). A = 10 x log10(Po / Pi) dB, Where Pi is the input power and Po the output power
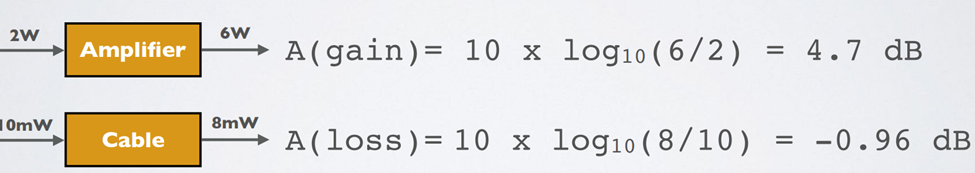
· To convert decibel to power ratio: Po/Pi = 10(A/10)
· The logarithmic scale is used to avoid very big or very small numbers, meaning the ratios. Using decibels is easier to work with.
· For example: A power ratio of 1,000,000 (1 million) can be expressed by 60 dB. A power ratio of 0,000001 can be expressed by -60 dB.
· A power ratio of 1,000,000,000,000,000 (1 quadrillion) can be expressed by 150 dB. A power ratio of 0,000000000000001 can be expressed by -150 dB.
· A power ratio of 1,000,000,000,000,000,000,000,000 (1 septillion) can be expressed by 240 dB.
· A power ratio of 0,000000000000000000000001 can be expressed by -240 dB.
dBm
· dB is a ratio it does not represent an absolute value.
· If we use a reference input power of 1mW (Pi =1 mW) the unit is expressed as dBm.
o A = 10 x log10(Po / 1) dBm
o Po/Pi = 10(A/10) => P = 10(A/10) mW
· Unit dBm represents an absolute value because it uses a fixed reference value of 1mW.

· There is an easy way to convert dBm values to its absolute power value (Po)
o Rules of !0 and 3
o 10 dB = *10
o -10 dB = /10
o 3 dB = x2
o -3 dB = /2

· You can calculate any number by only using the values 10 and 3.
o Only use a multiple of 10’s and 3’s (positive and negative) to represent a value.
o If possible, avoid using 3’s and never use more than five 3’s!
o Incorrect: 8 = 3 + 3 + 3 + 3 + 3 + 3 – 10
o Correct: 8 = 10 + 10 – 3 – 3 – 3 – 3


dBi, dBd
· Other notable decibel notations are: dBi and dBd (these also represents ratios)
· Antenna manufacturers are using these units to measure antenna performance and it is useful for comparison purposes.
o Manufacturer A has an 868MHz antenna, its gain is 3 dBi
o Manufacturer B has an 868MHz antenna, its gain is 2.5 dBi
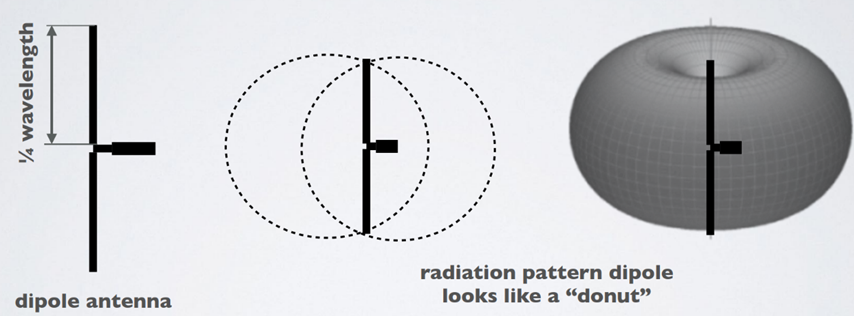
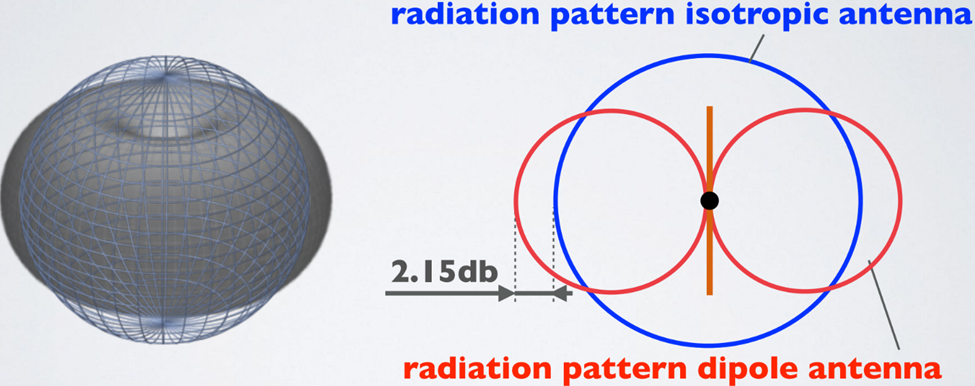
· dBi refers to the antenna gain with respect to an isotropic antenna. This is a hypothetical point source antenna, that radiates its power uniformly in all directions.

· dBd refers to the antenna gain with respect to a reference dipole antenna.
· The relationship between dBd and dBi is dBi = dBd + 2.15
Propagation
Propagation is the way radio waves travel through free space (also known as medium). The way these waves travel may impact its signal strength.
· Line-of-sight propagation The radio waves travels directly from sender to receiver without any obstacles. If the distance between sender and receiver gets larger, the signal will get weaker. This loss is known as Free Space loss

· If there are obstacles near its path (within the Fresnel zone), the radio waves reflecting off those objects may arrive out of phase with the signals that travel directly and reduce the power of the received signal.

· Propagation through obstacles Radio waves may penetrate thru obstacles that appear in its path. Radio waves lose strength if they travel through obstacles made of more conductive materials.
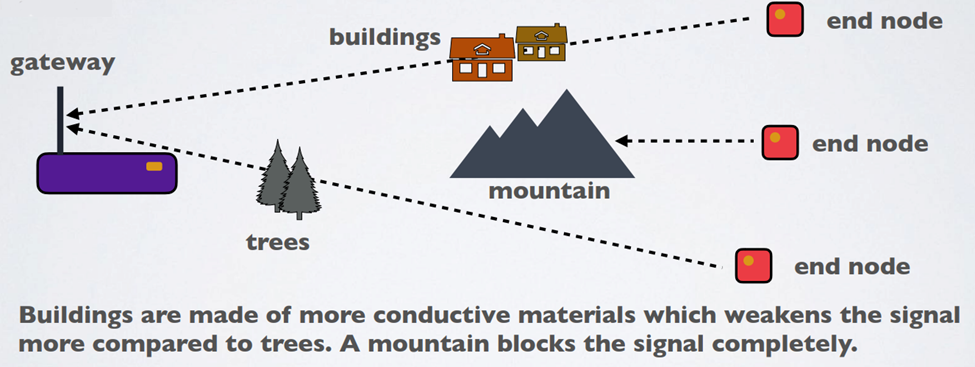
· Propagation through diffraction. Diffraction is where radio waves are bent around sharp edges. A signal from a transmitter may be received by the gateway even though it may be “shaded” by a large obstacle.
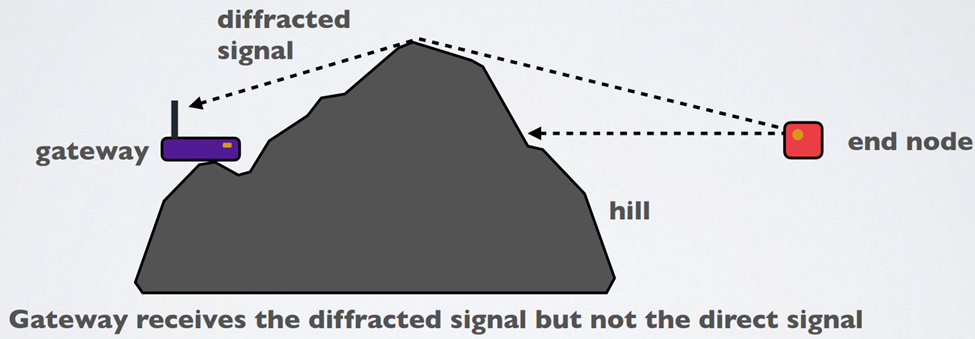
There are more types of propagations which impact the signal strength but these are the important ones.
Free Space Loss
The free space loss can be calculated as follow:
Lfs = 32.45 + 20xlog(D) + 20xlog(f)
Lfs = Free space loss in dB
D = Distance between end node and gateway in km
f = frequency in MHz
Example
· D=0.01 km, Lfs=32.45+20xlog(0.01)+20xlog(868) = 51 dB
· D=0.05 km, Lfs=32.45+20xlog(0.05)+20xlog(868) = 65 dB
· D=0.10 km, Lfs=32.45+20xlog(0.10)+20xlog(868) = 71 dB
· D=0.50 km, Lfs=32.45+20xlog(0.50)+20xlog(868) = 85 dB
· D=1.00 km, Lfs=32.45+20xlog(1.00)+20xlog(868) = 91 dB