PID Controller

Introduction

• Definition: A Proportional-Integral-Derivative (PID) Controller is a feedback control system commonly used to maintain a desired output in various processes. It combines the proportional, integral, and derivative controls, each addressing a specific aspect of the control process to ensure precise, stable, and efficient performance.
• Importance: PID Controllers are essential in industrial and automation processes where precise control is necessary, such as temperature regulation, motor speed control, and process control.

Working Principle

• The PID Controller uses three terms – Proportional (P), Integral (I), and Derivative (D) – each with a distinct role in controlling the output.
• Control Equation:
• 
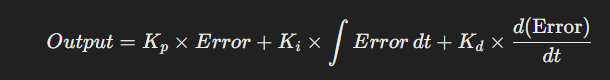
• where:
• Kp: Proportional gain.
• Ki​: Integral gain.
• Kd​: Derivative gain.
• Error: The difference between the setpoint and the current process variable (output).
• Explanation of Each Component:
• Proportional (P) Control:
• Reacts to the current error and applies a corrective action proportional to the magnitude of the error.
• High Kp​ leads to faster response but can cause overshoot.
• Integral (I) Control:
• Accumulates the error over time to eliminate any steady-state error.
• Helps ensure that even small errors are corrected, preventing drift away from the setpoint.
• Derivative (D) Control:
• Predicts future errors based on the rate of change of error.
• Provides a damping effect, reducing overshoot and improving stability.

Advantages and Disadvantages of PID Controller

• Advantages:
• Combines the benefits of all three controllers, offering precise control.
• Effective in minimizing steady-state error, reducing overshoot, and stabilizing the system.
• Versatile and widely applicable in different control environments.
• Disadvantages:
• Can be challenging to tune correctly, as finding the right gains for each component can take time.
• Sensitive to noise, particularly the derivative component.
• May not perform well in non-linear or highly dynamic environments without advanced tuning.

Applications of PID Controller

• Temperature Control: Maintaining stable temperatures in HVAC systems, ovens, and industrial processes.
• Motor Speed Control: Regulating the speed of motors in various machines and vehicles.
• Flow Control: Managing the flow rate of liquids or gases in chemical and process industries.
• Positioning Systems: Precise control in robotic arms and CNC machines for accurate positioning.

Example of PID Controller: Temperature Control System

• Objective: Maintain the temperature of a furnace at a constant setpoint.
• Setup:
• Sensor: Measures the current temperature inside the furnace.
• PID Controller: Adjusts the heating element’s power to maintain the setpoint temperature.
• Implementation:
• Measure the current temperature and calculate the error as the difference between the setpoint and measured temperature.
• Apply each PID term:
• Proportional: Responds to the current error by adjusting power proportionally.
• Integral: Accumulates the error over time, ensuring no deviation from the setpoint in the long term.
• Derivative: Anticipates future errors based on the current rate of temperature change, helping to prevent overshoot.
• Combine the effects of all three terms to determine the final control output.
• Expected Outcome: The PID Controller smoothly maintains the furnace at the setpoint temperature with minimal overshoot and no steady-state error.

Tuning the PID Controller

• Manual Tuning: Adjust Kp, Ki​, and Kd​ values manually, observing system response and adjusting accordingly.
• Ziegler-Nichols Method: A more systematic approach where gains are set based on specific response criteria.
• Software Tools: Some applications use tuning software to automatically adjust PID values for optimal performance.

Conclusion

• The PID Controller provides a powerful, adaptable, and efficient approach to control across many systems, effectively combining the P, I, and D components for robust performance. While tuning can be complex, once optimized, PID Controllers can provide reliable and precise control over a wide range of applications.